Abbiamo già introdotto al Calcolo differenziale nella pagina sulle derivate: oggi andiamo a vedere l’altra faccia di queste operazioni, ovvero gli integrali.
Aree e funzioni
Se prendiamo una funzione e un determinato intervallo del parametro, possiamo chiederci quanto valga l’area delimitata proprio dalla funzione, dall’asse x e dagli estremi di questo intervallo.
L’operazione che ci permette di calcolare quest’area è proprio l’integrale: cerchiamo di costruire questa operazione a partire dalle aree di funzioni semplici.
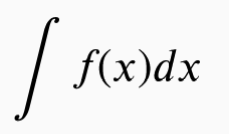
La funzione più semplice che possiamo immaginare è una funzione costante y=k, rappresentata da una retta orizzontale: se noi cerchiamo di calcolare l’area “sottesa” a questa funzione tra x=0 e un valore x positivo qualunque, ciò che trovo è un rettangolo alto k e largo x, la cui area è evidentemente kx.
Prendiamo quindi un’altra funzione molto semplice, y=x: stavolta ci troviamo di fronte all’area di un triangolo, che è ½ base per altezza, cioè ½ x^2.
Quindi l’integrale di y=k è kx e quello di y=x è ½ x^2… se andiamo a prendere questi due risultati e ne applichiamo la derivata, ritroviamo proprio le funzioni di partenza!
E’ possibile dimostrare che questo è vero in generale: integrale e derivata sono funzioni inverse, applicando una all’altra si torna sempre alla funzione di partenza.
Calcolare un integrale
Esattamente come la derivata di un termine noto è 0, e quindi funzioni con diverso termine noto hanno la stessa derivata, è possibile ribaltare questo concetto dicendo che da una funzione si possono ottenere infiniti integrali detti “indefiniti” che differiscono solo per una costante, la cosiddetta “costante di integrazione” (di solito si usa la lettera C maiuscola): nel momento però in cui definiamo, come nel disegno iniziale, un intervallo specifico nel quale calcolare il mio integrale, questa costante acquisisce un valore specifico che dipende da questi “estremi di integrazione” (il cosiddetto “integrale definito”).
Per quanto riguarda solo i polinomi, possiamo ribaltare l’algoritmo usato per le derivate:
- Lavoriamo con i singoli monomi: l’integrale sarà la somma dei nostri risultati
- Per integrare un monomio:
- Aumentiamo di 1 l’esponente dell’incognita, se assente la aggiungiamo di primo grado
- Dividiamo per l’esponente aumentato
- Infine aggiungiamo la costante di integrazione C
Quindi, riprendendo l’esempio usato per le derivate, se vogliamo integrare y’=-2x+3 (che abbiamo ottenuto derivando y= -x^2 +3x +2):
- Il termine -2x aumenta di uno il grado e poi si divide per il nuovo esponente: otteniamo quindi -x^2
- Il termine 3 vede l’aggiunta della x, per poi dividere per il nuovo grado (1), quindi semplicemente 3x
- Aggiungiamo infine la costante di integrazione C.
Mettendo i pezzi assieme, otteniamo la funzione y= -x^2 +3x +C.
Esattamente come tutte le funzioni che differiscono solo per una costante hanno la stessa derivata, così integrando la stessa derivata posso ottenere infinite funzioni, differenti solo per il valore di C: nel caso specifico in cui C=2 otteniamo esattamente la funzione di partenza
Un integrale abbastanza diffuso in fisica, che rispecchia il rapporto tra la variazione di un valore e il suo totale sommato su tanti contributi, è il seguente:
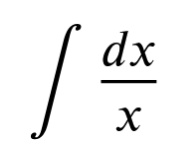
Questo integrale da come risultato il logaritmo naturale del valore assoluto di x, più una costante: in breve ln(|x|) +C
