Monomi e Polinomi

La matematica ti riusciva finché non ci hanno infilato le lettere? Questo articolo ti aiuterà a capire come funzionano le incognite e una delle loro applicazioni più diffuse, i polinomi!
I polinomi hanno molte applicazioni in fisica: questo articolo ti aiuterà a capire cosa sono e come funzionano i polinomi.
Attenzione però: per diventare capace a usarli dovrai fare esercizi e, probabilmente, fare riferimento anche ad altro materiale. In fondo all’articolo, tuttavia, troverai alcuni semplici esempi!

Le Incognite e il loro uso

• Le incognite sono valori inizialmente sconosciuti all’interno di un’espressione matematica: sono rappresentate da lettere e ci permettono di formulare problemi che descrivono matematicamente situazioni del mondo reale, rendendole comprensibili e risolvibili
  Ad esempio potremmo chiamare “t” il tempo necessario per cucinare una pietanza.
• In linea generale le incognite possono nascondere ogni genere di numero: numeri positivi e negativi, interi o decimali, frazioni, radici quadrate e così via.

Cos’è un Monomio 

• Un monomio è un singolo termine ottenuto da una parte letterale (ovvero una o più incognite) e/o da una numerica: quando sono entrambe presenti, sono moltiplicate tra loro.
  Quindi “x” è un monomio, così come lo è “3”, ma anche “3x”, che è una maniera compatta per scrivere “3 per x”. 
• La parte numerica si dice “coefficiente” del monomio: se non specificata (es: “x”) è pari 1.
• Le singole incognite possono anche mostrare degli esponenti, ovvero un numero in alto a destra che sta a intendere quante volte ho moltiplicato l’incognita per se stessa: si tratta di una vera e propria potenza come per 3² che è pari a 3 per 3, cioè 9.
  Quindi x² vuol dire x per x, stesso vale per x³ che rappresenta x per x per x…
  A differenza dei numeri, essendo le lettere delle incognite, noi non possiamo a priori sapere quanto vale x² perché non sappiamo quanto vale x e quindi non possiamo effettuare il calcolo.
• Se non specificato, una incognita da sola (es “x”) ha esponente “1”, mentre un monomio privo di incognita è come se avesse x⁰ (qualunque numero elevato alla 0 fa 1).
  L’esponente dell’incognita è detto grado del monomio: i monomi di grado 0 (senza incognita esplicita) si chiamano termini noti perché non contengono incognite!

Operazioni tra monomi

• Possiamo moltiplicare tra loro due o più monomi, facendo separatamente il prodotto delle parti numeriche e di quelle letterali: moltiplicare più incognite tra loro si fa sommando gli esponenti.
  Quindi 5x per 4x fa 20x² perché ho moltiplicato tra loro le parti numeriche (5 per 4 = 20) e quelle letterali (x¹ per x¹ fa x²), esattamente come 2 per 3x fa 6x² (in questo caso il primo monomio non mostra incognite, quindi è come se la parte letterale fosse x⁰).
• Se appaiono più incognite, si fa il prodotto di quelle uguali e si scrivono separatamente quelle differenti: quindi 2ax per 5 bx fa 10abx².
• Se due monomi hanno la stessa, identica parte letterale si dicono simili e si possono anche sommare o sottrarre, facendo somme e sottrazioni con le loro parti numeriche: in questo caso le parti letterali agiscono come se fossero “oggetti” da sommare.
  Quindi noi possiamo dire che 2 mele più 3 mele fa 5 mele esattamente come diciamo che 2x + 3x = 5x.

Polinomi

• Quando ho la somma di più monomi non simili, non posso sommarli tra loro e devo lasciarli separati ad esempio 3x + 2y: in questi casi mi trovo di fronte a un Polinomio!
• Spesso si lavora in algebra con polinomi che mostrano una sola incognita, oltre ai termini noti, ma a potenze differenti: per esempio il polinomio 3x² + 2x + 3 è composto da tre monomi non simili tra loro, quindi non può essere ulteriormente “ridotto”, e mostra una sola incognita (x) a varie potenze.
• il grado di un polinomio in una sola variabile è pari a quello massimo tra i monomi che lo compongono. Ad esempio, il polinomio 3x²– x – 5 ha grado 2 (“secondo grado”), poiché il termine 3x² ha l’esponente più alto (2).

Equazioni e Polinomi

• Un’equazione algebrica è un confronto di uguaglianza tra due polinomi: un esempio molto semplice potrebbe essere 5x = 20, che potrebbe rispondere alla domanda “voglio comprare dei panini che costano 5 euro l’uno, con 20 euro quanti ne posso comprare?”.
• Le espressioni matematica a destra e a sinistra dell’uguale si chiamano membri dell’equazione.
• Un’equazione algebrica è risolta quando ho trovato il valore (o i valori) dell’incognita che rendono vera l’uguaglianza. In questo caso, per il valore di x=4, l’equazione risulta essere 5 per 4 uguale 20, che è ovviamente vero: “x=4” è quindi la soluzione dell’equazione.
• Lo strumento principale che usiamo per risolvere le equazioni sono i cosiddetti principi di equivalenza: questi principi ci permettono di trasformare l’equazione mantenendo però le stesse soluzioni. Risolvere quindi l’equazione modificata ci darà gli stessi risultati dell’originale.
• Tra le conseguenze di questi principi c’è la possibilità di spostare singoli monomi o intere espressioni da un membro all’altro cambiandone il segno: se questo lascia un membro sprovvisto di termini, esso è pari a zero.
  Nell’esempio precedente, l’equazione 5x=20 può diventare 5x-20 =0
• I valori delle x che risolvono un’equazione del tipo “Polinomio = 0” si dicono “Zeri del polinomio“ perché, sostituendo tale valore alla x, il risultato mi fa 0.
  Se sostituiamo la x trovata precedentemente otteniamo 5 per 4, meno 20, che fa zero.
• Un polinomio può avere 0, 1 o più “Zeri”: il numero massimo di zeri di un polinomio è uguale al suo grado. Quindi, un polinomio di grado 2 può avere al massimo due zeri.
  Per un’equazione “Polinomio = 0”, trovare gli zeri significa risolvere l’equazione e viceversa.
  Il polinomio “5x-20” è di primo grado e quindi ha un solo zero, cioè una sola soluzione all’equazione “5x-20=0”, che è quella che abbiamo precedentemente trovato (x=4).
  Il polinomio “x²-4” è di secondo grado e quindi ha al massimo due zeri, cioè due soluzioni all’equazione “x²-4=0”: sono i valori x = 2 e x = -2.
  Infatti 2 alla seconda fa 4, -4 = 0. ma anche -2 alla seconda fa 4 ed è anch’esso soluzione.

BONUS: Risolvere un’equazione di primo grado

Dai principi precedentemente elencati discendono alcune conseguenze che useremo per risolvere un’equazione di esempio:

3x – 5 = x + 1

Una conseguenza del primo principio mi permette di spostare singoli monomi da un membro all’altro, cambiandogli di segno. Lo uso quindi per portare tutti i termini con x a sinistra e i restandi a destra

3x – x = 5 + 1

Chiaramente questi monomi sono simili, quindi posso sommarli

2x = 6

A questo punto divido entrambi i termini per 2, che equivale a portare a denominatore del secondo membro il coefficiente a moltiplicare del primo membro

x = 6/2 = 3

Ovviamente questi passaggi non hanno alterato la soluzione dell’equazione: se infatti sostituiamo 3 alla x nella forma originale dell’equazione otteniamo 9 – 5 = 3 + 1 che è altrettanto vera.

BONUS: Risolvere un’equazione di secondo grado

Le equazioni di secondo grado richiedono un metodo più complesso: storicamente vengono risolte con un metodo geometrico (“completamento del quadrato”), ma noi useremo la formula che si insegna a scuola è che è stata sviluppata per la prima volta da Brahmagupta, un matematico indiano del settimo secolo DC.

Un’equazione di secondo grado potrà essere sempre portata in una forma in cui avrò un polinomio di secondo grado a sinistra dell’uguale e lo zero a destra: sarà inoltre possibile avere al massimo un termine di secondo grado, uno di primo e un termine noto (nel caso in cui fossero di più, posso sommarli essendo monomi simili).

Quindi, tutte le equazioni di secondo grado possono essere riportate nella forma: ax² + bx + c = 0

In questa forma, abbiamo chiamato a, b e c rispettivamente il coefficiente di secondo grado, di primo grado e il termine noto.

Questa equazione può avere due soluzioni separate, due soluzioni coincidenti oppure nessuna soluzione: la formula sviluppata da Brahmagupta ci permette di trovare le soluzioni con la seguente espressione.

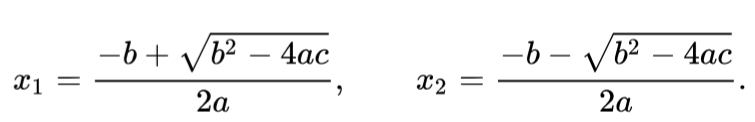
Se il termine sotto radice (chiamato “Delta”) è positivo, le due soluzioni saranno differenti; se è uguale a zero, saranno uguali; se è negativo, non sarà possibile effettuare con i numeri reali la radice quadrata di un numero negativo e quindi non troverò soluzioni all’equazione.

Prendiamo un’equazione risolvibile: x² + 5x + 6 = 0

Risulta evidente che il termine a=1, b=5, c=6. Il “Delta” è pari a 5² – 4(1)(5) = 25-24 = 1, la cui radice è 1.

Le soluzioni sono quindi (-5+1)/2 e (-5-1)/2, ovvero x = -2 e x = -3.